Math problem - Circles

http://www.roytanck.com/2016/01/04/math-problem-why-does-this-work/

Roy states the following problem The length of the white area, which composes the outer shape if for each circle: d= (360/number_of_circles_in_graph)*2 , where d = degrees.
This is more or less correct.

Now let's look at that.
For 0 circles it would be (360/0)*2=infinity degrees. You go around endlessly.. ok..
For 1 circle it would be (360/1)*2=720 degrees. You go around twice.
For 2 circles it would be (360/2)*2=360 degrees. You go around once.
For 3 circles it would be (360/3)*2=240 degrees. You go around 2 thirds.
For 4 circles it would be (360/4)*2=180 degrees. You go around half a circle
For 5 circles it would be (360/5)*2=144 degrees. you go around 2 fifths of a circle.
If you don't look too hard at the first cases with one circle and zero circles it works.
Why?

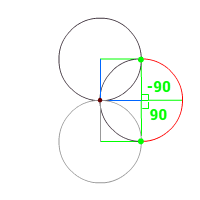
The circle are rotated around a point, let's call that x:0,y:0 or o. (dark red)
In the case of four circles, we create the first circle at 0,0, at an angle of 0 degrees.
And place the midpoint away from o.
How far: exactly the radius of the circle.

The previous circle will be at 360/4= -90 degrees. Also placed a distance of the radius away from o.

To get to the 'outline' we have to look at the next circle as well at 90 degrees.

The green point is at the beginning of the arc along the current circle, that together with the arcs on the other circles form the 'outline'. (The red bit)
The startpoint of this arc must be on both the next (top) and current circle (left).
There are only two points, that qualify. o (dark red), which is by definition 'inside' and the green point.

Because the point is on both circles, the angle from the midpoint of the current circle to the green point is 90 degrees. This angle echos the creation of the circles: It's a repetition of the circle's original rotation.

The same must be true for the previous circle at 90 degrees. To get the total angle of the arc: from -90 to 90 = 180 degrees.
This is true for 4 circles, but it works for any amount of circles higher that 2. (2 itself is a bit mind-bending, but I think the same principle applies)

To show you this is true, we look at the situation for 5 circles. The angle to get the next circle is -72
 -(360/5) and the angle to get the previous one is 72 (360/5). (or the other way around, depending in which direction you draw your circles)
If you set up the lines again, you see that the 'outer' arc must be those two angles combined, so 2* 360/5= 2*72=144
Your formula is implied in the problem.

NOW>>>
If the circles did NOT intersect at the origin this formula wouldn't work.
The formula would then be d=(360/nr_of_circles+a)*2
Where 'a' would be a function of the (distance to the origin of the midpoint - radius of circle) or the distance to the closest point on the circle and having a range, because at some point the circles would stop touching at all. This range would be zero to zero for two circles and slightly bigger for each additional circle, with a limit at a zero to triple the circle radius (where no circles would ever touch).